A. Number

personalized jerseys
nike air jordan 11 legend blue
adidas promo code
adidas yeezy foam runner
adidas yeezy foam runner
nike air max
adidas yeezy boost 700
wig store
seahawks nfl
custom football jerseys
custom soccer jerseys
mens nike air jordan
human hair wigs
Human hair Wigs
cheap nfl jersey

Subtask 1,3

对于Subtask 3，我们计算发现 10^k+x\le 2\times10^{18}，因此我们可以使用long long保存 10^k，直接计算结果。

如何计算 10^k 呢？这里有三种写法：

• 一个for循环将一个初始为 1 的变量进行 k 次乘 10。
• 预处理出pw[20]={1,1e1,1e2,1e3,1e4,...,1e18}。
• 使用math.h或者cmath库内的pow(10,k)

注意：使用后两种写法，处理结果是double型，请强制转long long或者%.0lf输出。

Subtask 1是留给忘记开long long，只开了int的同学的。

Subtask 2

我们先假设 k>0，选几个数看看——

10^9+7=1000000007，这里一共 8 个零。

我们观察一下 10^9+7=1000000007，发现中间有 8 个零。

换一个数，10^6+0=1000000，可以看作 5 个零，后面补个 x。

因此先输出 1 ，后面跟 k-1 个零，最后输出 x。

务必注意上述条件成立当且仅当 k>0，你需要特判 k=0 的情况，也就是输出 x+1。

Subtask 4,5(I)

首先，如果 10^k\le x，直接计算。Subtask 4是留给忘记这个特判的同学的。

我们尝试进行一些小学生计算：

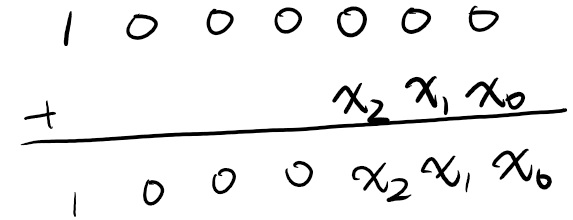
我们发现：假设数字 x 有 s 位，那么 10^k+x 就由一个 1 ，k-s 个 0，最后末尾加入 x 构成。

如何计算一个数 x 的位数呢？下面是几种常见写法：

• 定义变量 y，每次 y 变成原来的 \frac{1}{10}，s 就加一。特别注意：x=0 的情况需要特判。
• 用sprintf(ord,"%d",x)语句输出到char ord[]字符串中，然后使用strlen(ord)求长度。
• 使用floor(log10(x))+1计算位数。注意：下取整后加一，x=0 要特判。

Subtask 4,5(II)

这里主要讲一些特殊方法，一般同学稍作了解即可，不知道也没有问题。

Python大法

Python大法

Python由于自带高精，做这种事情自然是十分方便的。下面是参考Python3代码：

a=input().split()
print(pow(10,int(a[0]))+int(a[1]))

C++自带函数法

我们观察这个竖式，可以将 10^k>x 的情况换一种形式：

> 先输出字符1，然后将 x 以固定的长度 k 输出，不足 k 位用前导零补齐。

在C/C++中，printf就可以上面的操作：

//在主函数中加入这句
printf("%019d",19810);

你的输出是不是0000000000000019810？

因此，如果我们要计算 10^{20}+x，我们可以这么写：

printf("1%020d",x);

为了让计算机自动给我们把 k 填入printf语句中，我们需要使用sprintf函数：

//假设k=6,x=35
char ord[15];
sprintf(ord,"1%%0%dlld",k);//想输出%要在语句中填入%%
//ord现在是"1%06lld"
printf(ord,x);//1000035

总结

这题主要考察分支结构，循环结构，还对字符、数学位值原理有一定的考察。

送分到位，部分分充足，解法多样有趣。

解法到底有多少呢？哪怕只计算C++的常见写法：

• 对于特判：k<18，k<=18，x的位数<=k三种；
• 乘方计算：乘 10 法，预处理法（科学计数/手打一大波0），pow法四种；
• 位数计算：除 10 法，log10法，sprintf+strlen法，sprintf+printf法四种。

3\times 4\times 4=48 种。

B

分类讨论题，部分分其实都是针对分类的一部分。

• 如果 a=b=0，不需要进行任何操作，答案为 0。
• 如果 a=0,b\neq 0，使用一次操作 2 将 a 乘 b+1，b 除以 b+1 即可，由于只使用操作 1 不会使得两数都变为 0，这样做总代价一定是最小的，为 d，a\neq 0,b=0 同理。
• 如果 a=b\neq 0，有两种方法，第一种是使用一次操作 1，即可将两数都变为 0，第二种是使用两次操作 2，第一步将 a 乘 b+1，b 除以 b+1，这样 b 就变为 0 了，再将 b 乘 a+1（这里 a 是第一次操作后 a 的值），a 除以 a+1，即可使得两数都为 0，代价为 2\times d。由于不存在只使用一次 2 操作的方案（这样的话总代价为 d），答案必为两者中的较小值 \min(c,2\times d)，其它任何方案代价一定大于等于该值。
• 如果 a\neq b,a\neq 0,b\neq 0，有两种方法，第一种是用两次操作 2，与上面所说的相同，第二种是先用一次操作 1 将 a 和 b 中较小的那一个变为 0，再用一次操作 2 把另一个数变为 0，代价为 c+d，由于不存在只使用一次操作 1（总代价为 c）或只使用一次操作 2（总代价为 d）的方案，答案必为两者中的较小值 \min(c+d,2\times d)。

C

第一个点枚举 k 去判是否满足即可 第二个点枚举 k 的时候初始化求出小于等于每个 m 的答案，询问时 O(1) 第三个点 a_i 特别大，如果不能消掉大的部分就是-1，否则 k 的那一位一定是 1 第四五六个点的做法和正解差不多，只是最后用背包而不是贪心 将所有 a 换成二进制，统计每一位上有几个数为 1 ，这样问题就转换成有若干个物品， 每个物品花费 2 的若干次方，得到的价值为 2 的若干次方乘上一个数，每种物品有两个形态， 一个形态表示 k 这一位为 0 ，则价值乘上的数为 a 中这一位为 1 的数的个数， 另一个形态表示 k 这一位为 1 ，价值乘上的数为 a 中这一位为 0 的数的个数。 一开始我们先贪心求出一个 k 使 \sum a \, xor \, k 最小，这个贪心是显然的， 之后我们从高位往低位贪心求 k ， 如果这一位 k 已经为 1 ，则不用管直接继续下一位， 如果这一位 k 为 0，那么贪心取， 如果这一位 k 为 1 的价值加上已有价值小于等于 m 的话，那这一位一定为 1 ， 否则 k 这一位一定为 0 （为 1 就不符合题意了）最后输出得到的 k 就是答案 注意一下数据，这个数据很大，看似需要高精度，实际上只需要一个特判就可以判掉无解 使用 int128 也是可以的 时间复杂度 O(50(n+q))

D. Fallen Lord

Subtask 1

O(m^n) 大暴力搜索，甚至不用剪枝。

Subtask 2

读题分，输出 n-1。

Subtask 3

所有边都取两个端点的 a 值的 min，相加即可。

Subtask 4

发现点 u 周围的边权的中位数不超过 a[u] 的充要条件是 ：

u 周围的边权中有不少于 \lfloor\dfrac{d[u]}{2}\rfloor 个 \le a[u] 的数，相当于有不超过 \lfloor\dfrac{d[u]-1}{2}\rfloor 个 >a[u] 的数。

令 up[u]=\lfloor\dfrac{d[u]-1}{2}\rfloor。

其中 d[u] 表示 u 的度数。

假设那个度数为 n-1 的点是 u，剩下的点的集合是 \{v\}。

容易发现 v_i 的父边的权值 \le a[v_i]。

那么按照 a[v_i] 从大到小排序，接下来分类讨论：

• 如果有 > up[u] 个 > a[u] 的，那么取最大的 up[u] 个 a[v_i]，剩下的都取 min\{a[u],a[v_i]\}，相加。
• 否则的话，直接把所有 a[v_i] 相加。

当然也可以不排序，运用 nth\_element 就能做到 O(n)，这里不再赘述。

Subtask 5

考虑 dp。

dp[u][state] 表示 u 节点周围的状态为 state，0 表示 \le a[u]，1 表示 >a[u]。

需要保证这个 state 的 0 次位是他的父边的状态。

记录 max[u][0/1] 表示对于所有 0 次位为 0/1 的 state，dp[u][state] 的最大值。

对于每一个 v_i 分别求出它的父边 \le a[u] 和 >a[u] 时对 u 的最大贡献 val[i][0/1]，这个只需分类讨论即可。

接下来考虑计算 dp[u][state]，那么 state 的 1\sim d[u]-1 次位就对应着 u 的每一个儿子的父边的状态。

• 如果 state 第 i 位为 0，那么 val[i][0] 产生贡献。
• 否则 val[i][1] 产生贡献。

计算完所有 dp[u][state] 之后 max[u][0/1] 也很容易计算了。

时间复杂度 O(n\times 2^{max\{d[u]\}})

Subtask 6

发现并不关心具体是哪些边，可以考虑换一种方式 dp。

dp[u][i] 表示 u 的所有子节点的父边中有 i 个权值 >a[u]，u 的子树中边权和的最大值。

发现当 1\le i<up[u] 时，当前状态中 u 的父边可以 >a[u]，否则当前状态中 u 的父边只能 \le a[u]。

那么也就相当于这么一个问题：有 n 组物品，每组中都有 2 个不能同时选的物品。

第 i 组中有 1 个花费为 0 ，价值为 val[i][0] 的物品以及 1 个花费为 1 ，价值为 val[i][1] 的物品，

于是 u 节点的所有状态就能用普通的背包转移了。

时间复杂度 O(n^2)。

Subtask 7

考虑优化 dp 状态。

dp[u][0/1] 表示 u 节点的父边权值 能 / 不能 >a[u]，u 的子树中边权和的最大值。

同样求出 val[i][0] 和 val[i][1]，此时发现这个问题可以贪心解决。

现在相当于有初始价值 \sum val[i][0] 以及一些物品，每个物品花费都是 1，第 i 个价值为 val[i][1]-val[i][0]。

对于 0\sim up[u] 中的每一个数求出能获得的最大总价值。

那么直接按照 val[i][1]-val[i][0] 从大到小排序，将后面 <0 的舍弃掉，贪心求前缀和即可。

此时 dp 值也很容易就能计算出来。

时间复杂度 O(n\log n)，可以通过本题。

当然也可以不排序，运用 nth\_element 就能做到 O(n)，这里不再赘述。

E. Yoshino

Subtask 1

考虑暴力修改，暴力查询逆序对，复杂度 \operatorname O(n^3)。

Subtask 2

将逆序对改用归并排序或权值树查询，复杂度 \operatorname O(n^2\log n)。

Subtask 3

由于修改长度是 1，直接考虑使用树套树维护动态逆序对。在修改时查询 [1,l-1] 区间大于原数的和 [r+1,n] 区间小于原数的数的个数并减去，然后对新数做类似的查询并加上。在查询逆序对时，可直接输出。复杂度 \operatorname O(n\log^2 n )

Subtask 4

显而易见，在值域缩小的同时，修改区间也随之缩小。

于是我们可以考虑对每个值建一个树状数组，如果对应位置有这个值，则树状数组该位置的值就是 1，否则是 0。

在修改时，对 [1,l-1] 区间的每个值分别做一个查询并做一个后缀和，对 [r+1,n] 区间的每个值也做一个查询并做一个前缀和，然后对每个值，我们就可以用 \operatorname O(1) 的复杂度修改并维护了。

注意不要忘了清楚修改区间内部对逆序对的贡献，这部分可以暴力。

由于值域可以认为是 \operatorname O(\log n)，故此处的复杂度为 \operatorname O(n\log^2 n)。

Subtask 5

由于第两次操作一就会重置一次，我们可以考虑直接用数学方法计算出修改的贡献。

对于奇数次操作，直接重置，逆序对清零。

对于偶数次操作，分为 l<x 和 l>x 两种。

如果 l<x，则我们修改完后的该区间的值为 [x,x+r-l]，易知 [l,r] 与 [x,x+r-l] 的交集为 [x,l-1]。

则对于值在 [x,l-1] 区间的数，对逆序对的贡献显然是一个公差为 -1 的等差数列，我们可以直接对此进行求和。

而对于值在 [l,x-r+l] 区间的数，显然对逆序对没有贡献，直接忽略。

如果 l>r 则类似讨论。

于是，我们就可以 \operatorname O(1) 完成对逆序对个数的计数（注意此时我们并不需要直接修改这个数列），复杂度 \operatorname O(n)。

Subtask 6

考虑颜色段均摊。

这是一种类似于珂朵莉树的 trick（事实上这就是珂朵莉树的推平操作），复杂度为均摊 \operatorname O(n\times k)，其中 k 为单次修改的复杂度。

对于一个区间染色的操作，我们可以直接将一个区间维护为一个点，并且将他装入在 set 或其他容器中。

在修改时，我们在 set 中找到我们需要清除的所有区间（如果边界被包含则将边界所在的区间断开变成两个区间），并暴力将它们逐个清除，再插入新的区间。

为什么这样做的复杂度是正确的呢？我们可以来证明一下。

最初的时候，每个数单独构成一个区间，所以一共有 n 个区间。

而每次操作的时候，我们增加的区间包括断开左右边界区间时增加的两个区间，以及插入的新区间。

这样一来，整个操作过程中区间的总个数就是 n+3m 个。

而显然一个区间最多被插入一次，删除一次，且 nm 同级，所以复杂度为均摊 \operatorname O(n\times k)。

本题中的操作一并不是颜色段均摊，但显然可以用类似的方法，均摊 \operatorname O(n\times k) 完成修改。

但我们在修改的同时，还需要再维护一个动态逆序对，于是考虑令 k=\log^2n，使用树套树修改

考虑插入一个新段对逆序对的贡献（删除就将贡献减去）。

假设这个区间是 [l,r]，这个区间的值的范围是 [x,y](r-l=y-x)。

那么我们大致可以其他的数分为以下几类：

1. 位于 [1,l-1] 区间且值小于 x 的数。这类数没有贡献，直接无视。
2. 位于 [r+1,n] 区间且值大于 y 的数。这类数同样没有贡献，直接无视。
3. 位于 [1,l-1] 区间且值大于 y 的数。这类数对区间内的所有数都有贡献，只需统计个数并乘以 r-l+1。
4. 位于 [r+1,n] 区间且值小于 x 的数。这类数同样对区间内的所有数都有贡献，处理方法同上。
5. 位于 [1,l-1] 区间且值位于 [x,y] 之间的数。注意到，对于值为 t(t\in[x,y]) 的数，它对这个区间的贡献为 t-x，因为这个区间内前 t-x 个数的值会小于 t-x。于是我们可以对权值维护区间内的个数以及区间和，也就是一个范围内值在某个区间的数有几个，以及这几个数加起来是多少。然后用和减去个数乘以 x 就是我们所要的结果。
6. 位于 [r+1,n] 区间且值位于 [x,y] 之间的数。处理方式类似于第五类数。

这样一来，我们就在修改的同时完成了对逆序对的维护，而复杂度没有发生变化。

于是最终的复杂度就是 \operatorname O(n\log^2 n)。

总结

本题的难度并不高，没有涉及到很复杂的维护方法，也没有涉及到很高级的数据结构，主要还是对一些基本技巧的灵活应用。另外，有一个颜色段均摊的操作值得大家掌握。

为良心的出题人点赞！

F

性质 1

将这个图分成 nm 个 2 \times 2 个正方形，那么每个正方形中恰好有一个 1 \times 2。

证明：称 S 为所有被 1 \times 2 覆盖的格子的集合，那么 |S|=2mn。每个这样的 2 \times 2 中至多有两个格子属于 S。

然而所有 4mn 个格子中，恰好有一半的格子属于 S。所以每个 2 \times 2 中恰好 2 个，构成一个 1 \times 2。

从左上角的格子开始依次考虑，可以证明这些就是所有的魔力之石。

根据这个性质，称一个上述的分割中的 2 \times 2 的方格为 上，下，左，右 之一，取决于 1 \times 2 在它中的位置。

性质 2

一个 上 的方格的上方的方格也是 上 的，右边是 上 或者 右，左边是 上 或者 左。其他四种方格类似。

证明显然。

那么，结合以上两条性质，这个图大概是长这样的：

注意到，如果现在就要推式子等方法计算的话，这个生成函数肯定是二元的形式，难以计算，可以用矩阵做到 \Theta(n^6 \log m) 的复杂度，不详细说明。

这一步需要极高的技巧，相当于因式分解了那个难以刻画的二元生成函数。

用两条路径刻画这个图，一条从左上到右下，一条从左下到右上：

那么分成的四块就恰好是 上，下，左，右。

现在这题变成：左上走到右下，每次向右或者向下，有些地方不能走，求方法数。

不能走是因为有 k 个指定的位置，那么这些会限制这条路径。

当然，现在还没有明确说明哪些地方不能走，这里说清楚，下面的例子主要考虑左上到右下的路径。

限制就是，所有 下 的方格和所有 左 的方格和剩下两种方格被这条路径分成两半，也就是，如果把下和左看成 1，其余看成 2，那么这条路径将 1 与 2 分成两个部分。

现在让这个方格表左下为 (0,0)，右上为 (m,n)。如果一个 1 类方格的左下角为 (p,q)，那么这条路径不能经过任何 x\le p 并且 y \le q 的点，对于 2 类方格类似。下面的图表明了一种可能的能走与不能走的位置。

这里，红色的点表示不能走的点，绿色的线是一条合法的路径，黄色的线把能走到的地方分成了几个矩形。

矩形未必要有长与宽（可以为 0），可能用 s\times t 的点阵（ s,t \ge 1）来形容更加合适，下面 点阵 和 矩形 都代表这个意思。

这些矩形是有特殊要求的，不难发现不能走的地方构成了两个简单多边形，这两个多边形的边有水平的和竖直的，用竖直的边分割这个网格图得到了图中所示的矩形，后面的方法会说明为什么要这么分，可以通过上面的图更好的理解这些矩形是怎么刻画出来的。

当然，刻画这些矩形需要将所有放好的块排序并且利用单调栈维护，细节比较多，这里不细说。

考虑最基本的 dp 以及一个没有限制的图，令 dp[i][j] 为到 (i,j) 的合法路径数，那么 dp[i][j]=dp[i][j-1]+dp[i-1][j]。

这个式子可以化成 dp[i][j]=\sum_{k=1}^jdp[i-1][k]，也就是一个前缀和的形式。

注意到，如果按照上面的方式将合法区域划分为矩形，那么每个长为 t 的点阵就相当于做 t-1 次前缀和。

我们用到生成函数的知识，如果假设第 i 列（横坐标为 i 的所有点）从上到下的 dp[i][j](0 \le j \le n) 构成生成函数 F_i(x)=\sum dp[i][j]x^j，其中 0 \le i \le m，我们有递推式：

F_{i+1}(x)=\frac{F_i(x)}{1-x}，如果第 i 列与第 i+1 列在同一个矩形内；

如果不在同一个矩形内，一定在相邻两个矩形内，设这两个矩形的上下高度分别为 h_1,l_1,h_2,l_2，如图：

那么，这个生成函数，就是先保留原来 F_i(x) 在 h_2 到 l_1 次项的系数，然后对其做前缀和，为 G_{i+1}(x)，然后 F_{i+1}(x) 的系数，不大于 l_1 次项的与 G_{i+1}(x) 相同，l_1 到 l_2 次项用 G_{i+1}(x) 的 l_1 次项系数填充。

这个比较难以用式子进行刻画，所以只能通过文字进行解释。

我们并不需要求出所有的 F_i(x)，因为需要的甚至只是 F_m(x) 的一项系数，所以我们求出所有矩形两条宽所在列代表的多项式，相邻多项式之间的转移可以用多项式前缀和以及 NTT 优化就可以在 n \log n 的时间内完成，由于矩形一共 \Theta(n) 个那么这是 n^2 \log n 的，但是这不够优秀，瓶颈在求前缀和上。

如果不用做前缀和，剩下的操作甚至是 \Theta(n) 的。我们考虑一个稍微一般一点的问题：

维护一个多项式，支持三种操作：

（1）做若干次前缀和；（2）查一项系数；（3）加上一个单项式。

（在同一个矩形内的转移规约为（1）操作，相邻矩形转移可以查询 h_1 到 h_2 次项所有系数并依次减掉对应的单项式，然后再做一次前缀和，然后查询 l_1 次项的系数，最后在依次查询 l_1+1 到 l_2 次项的系数，把他们加上与 l_1 次项的系数的差）

此时解法几乎呼之欲出了：

维护一个多项式 Q(x) 与一个整数 t\ge 0，我们真实的多项式是 \dfrac{Q(x)}{(1-x)^t}，那么对于（1）操作直接修改 t，对于 2 操作可以 O(n) 求出卷积的一项，对于 3 操作将这个单项式乘以 (1-x)^t 后加到 Q(x) 上即可，时间复杂度 O(n^2)。