本文作者:Zhang, Xuheng
本文分类:Luogu 游记 浏览:1396
阅读时间:9377字, 约10.5-15.5分钟
注意:题解是md格式。
# A. Number
## Subtask 1,3
对于Subtask 3,我们计算发现 $10^k+x\le 2\times10^{18}$,因此我们可以使用`long long`保存 $10^k$,直接计算结果。
如何计算 $10^k$ 呢?这里有三种写法:
- 一个`for`循环将一个初始为 $1$ 的变量进行 $k$ 次乘 $10$。
- 预处理出`pw[20]={1,1e1,1e2,1e3,1e4,...,1e18}`。
- 使用`math.h`或者`cmath`库内的`pow(10,k)`
**注意:使用后两种写法,处理结果是`double`型,请强制转`long long`或者`%.0lf`输出。**
Subtask 1是留给忘记开`long long`,只开了`int`的同学的。
## Subtask 2
我们先假设 $k>0$,选几个数看看——
$10^9+7=1000000007$,这里一共 $8$ 个零。
我们观察一下 $10^9+7=1000000007$,发现中间有 $8$ 个零。
换一个数,$10^6+0=1000000$,可以看作 $5$ 个零,后面补个 $x$。
因此先输出 $1$ ,后面跟 $k-1$ 个零,最后输出 $x$。
务必注意上述条件成立当且仅当 $k>0$,你需要特判 $k=0$ 的情况,也就是输出 $x+1$。
## Subtask 4,5(I)
首先,如果 $10^k\le x$,直接计算。Subtask 4是留给忘记这个特判的同学的。
我们尝试进行一些小学生计算:
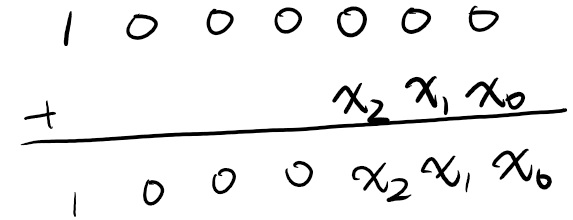
我们发现:假设数字 $x$ 有 $s$ 位,那么 $10^k+x$ 就由一个 $1$ ,$k-s$ 个 $0$,最后末尾加入 $x$ 构成。
如何计算一个数 $x$ 的位数呢?下面是几种常见写法:
- 定义变量 $y$,每次 $y$ 变成原来的 $\frac{1}{10}$,$s$ 就加一。**特别注意:$x=0$ 的情况需要特判。**
- 用`sprintf(ord,"%d",x)`语句输出到`char ord[]`字符串中,然后使用`strlen(ord)`求长度。
- 使用`floor(log10(x))+1`计算位数。**注意:下取整后加一,$x=0$ 要特判。**
## Subtask 4,5(II)
这里主要讲一些特殊方法,一般同学稍作了解即可,**不知道也没有问题。**
### Python大法
### Python大法
Python由于自带高精,做这种事情自然是十分方便的。下面是参考Python3代码:
```python
a=input().split()
print(pow(10,int(a[0]))+int(a[1]))
```
### C++自带函数法
我们观察这个竖式,可以将 $10^k>x$ 的情况换一种形式:
> 先输出字符1,然后将 $x$ 以固定的长度 $k$ 输出,不足 $k$ 位用前导零补齐。
在C/C++中,`printf`就可以上面的操作:
```c++
//在主函数中加入这句
printf("%019d",19810);
```
你的输出是不是`0000000000000019810`?
因此,如果我们要计算 $10^{20}+x$,我们可以这么写:
```c++
printf("1%020d",x);
```
为了让计算机自动给我们把 $k$ 填入`printf`语句中,我们需要使用`sprintf`函数:
```c++
//假设k=6,x=35
char ord[15];
sprintf(ord,"1%%0%dlld",k);//想输出%要在语句中填入%%
//ord现在是"1%06lld"
printf(ord,x);//1000035
```
## 总结
这题主要考察分支结构,循环结构,还对字符、数学位值原理有一定的考察。
送分到位,部分分充足,解法多样有趣。
解法到底有多少呢?哪怕只计算C++的常见写法:
- 对于特判:`k<18`,`k<=18`,`x的位数<=k`三种;
- 乘方计算:乘 $10$ 法,预处理法(科学计数/手打一大波0),`pow`法四种;
- 位数计算:除 $10$ 法,`log10`法,`sprintf+strlen`法,`sprintf+printf`法四种。
$3\times 4\times 4=48$ 种。
# B
分类讨论题,部分分其实都是针对分类的一部分。
- 如果 $a=b=0$,不需要进行任何操作,答案为 $0$。
- 如果 $a=0,b\neq 0$,使用一次操作 $2$ 将 $a$ 乘 $b+1$,$b$ 除以 $b+1$ 即可,由于只使用操作 $1$ 不会使得两数都变为 $0$,这样做总代价一定是最小的,为 $d$,$a\neq 0,b=0$ 同理。
- 如果 $a=b\neq 0$,有两种方法,第一种是使用一次操作 $1$,即可将两数都变为 $0$,第二种是使用两次操作 $2$,第一步将 $a$ 乘 $b+1$,$b$ 除以 $b+1$,这样 $b$ 就变为 $0$ 了,再将 $b$ 乘 $a+1$(这里 $a$ 是第一次操作后 $a$ 的值),$a$ 除以 $a+1$,即可使得两数都为 $0$,代价为 $2\times d$。由于不存在只使用一次 $2$ 操作的方案(这样的话总代价为 $d$),答案必为两者中的较小值 $\min(c,2\times d)$,其它任何方案代价一定大于等于该值。
- 如果 $a\neq b,a\neq 0,b\neq 0$,有两种方法,第一种是用两次操作 $2$,与上面所说的相同,第二种是先用一次操作 $1$ 将 $a$ 和 $b$ 中较小的那一个变为 $0$,再用一次操作 $2$ 把另一个数变为 $0$,代价为 $c+d$,由于不存在只使用一次操作 $1$(总代价为 $c$)或只使用一次操作 $2$(总代价为 $d$)的方案,答案必为两者中的较小值 $\min(c+d,2\times d)$。
# C
第一个点枚举 $k$ 去判是否满足即可
第二个点枚举 $k$ 的时候初始化求出小于等于每个 $m$ 的答案,询问时 $O(1)$
第三个点 $a_i$ 特别大,如果不能消掉大的部分就是$-1$,否则 $k$ 的那一位一定是 $1$
第四五六个点的做法和正解差不多,只是最后用背包而不是贪心
将所有 $a$ 换成二进制,统计每一位上有几个数为 $1$ ,这样问题就转换成有若干个物品,
每个物品花费 $2$ 的若干次方,得到的价值为 $2$ 的若干次方乘上一个数,每种物品有两个形态,
一个形态表示 $k$ 这一位为 $0$ ,则价值乘上的数为 $a$ 中这一位为 $1$ 的数的个数,
另一个形态表示 $k$ 这一位为 $1$ ,价值乘上的数为 $a$ 中这一位为 $0$ 的数的个数。
一开始我们先贪心求出一个 $k$ 使 $\sum a \, xor \, k$ 最小,这个贪心是显然的,
之后我们从高位往低位贪心求 $k$ ,
如果这一位 $k$ 已经为 $1$ ,则不用管直接继续下一位,
如果这一位 $k$ 为 $0$,那么贪心取,
如果这一位 $k$ 为 $1$ 的价值加上已有价值小于等于 $m$ 的话,那这一位一定为 $1$ ,
否则 $k$ 这一位一定为 $0$ (为 $1$ 就不符合题意了)最后输出得到的 $k$ 就是答案
注意一下数据,这个数据很大,看似需要高精度,实际上只需要一个特判就可以判掉无解
使用 $int128$ 也是可以的
时间复杂度 $O(50(n+q))$
# D. Fallen Lord
## Subtask 1
$O(m^n)$ 大暴力搜索,甚至不用剪枝。
## Subtask 2
读题分,输出 $n-1$。
## Subtask 3
所有边都取两个端点的 $a$ 值的 $min$,相加即可。
## Subtask 4
发现点 $u$ 周围的边权的中位数不超过 $a[u]$ 的充要条件是 :
$u$ 周围的边权中有**不少于** $\lfloor\dfrac{d[u]}{2}\rfloor$ 个 $\le a[u]$ 的数,相当于有**不超过** $\lfloor\dfrac{d[u]-1}{2}\rfloor$ 个 $>a[u]$ 的数。
令 $up[u]=\lfloor\dfrac{d[u]-1}{2}\rfloor$。
其中 $d[u]$ 表示 $u$ 的度数。
假设那个度数为 $n-1$ 的点是 $u$,剩下的点的集合是 $\{v\}$。
容易发现 $v_i$ 的父边的权值 $\le a[v_i]$。
那么按照 $a[v_i]$ 从大到小排序,接下来分类讨论:
- 如果有 $> up[u]$ 个 $> a[u]$ 的,那么取最大的 $up[u]$ 个 $a[v_i]$,剩下的都取 $min\{a[u],a[v_i]\}$,相加。
- 否则的话,直接把所有 $a[v_i]$ 相加。
当然也可以不排序,运用 $nth\_element$ 就能做到 $O(n)$,这里不再赘述。
## Subtask 5
考虑 $dp$。
$dp[u][state]$ 表示 $u$ 节点周围的状态为 $state$,$0$ 表示 $\le a[u]$,$1$ 表示 $>a[u]$。
需要保证这个 $state$ 的 $0$ 次位是他的父边的状态。
记录 $max[u][0/1]$ 表示对于所有 $0$ 次位为 $0/1$ 的 $state$,$dp[u][state]$ 的最大值。
对于每一个 $v_i$ 分别求出它的父边 $\le a[u]$ 和 $>a[u]$ 时对 $u$ 的最大贡献 $val[i][0/1]$,这个只需分类讨论即可。
接下来考虑计算 $dp[u][state]$,那么 $state$ 的 $1\sim d[u]-1$ 次位就对应着 $u$ 的每一个儿子的父边的状态。
- 如果 $state$ 第 $i$ 位为 $0$,那么 $val[i][0]$ 产生贡献。
- 否则 $val[i][1]$ 产生贡献。
计算完所有 $dp[u][state]$ 之后 $max[u][0/1]$ 也很容易计算了。
时间复杂度 $O(n\times 2^{max\{d[u]\}})$
## Subtask 6
发现并不关心具体是哪些边,可以考虑换一种方式 $dp$。
$dp[u][i]$ 表示 $u$ 的所有子节点的父边中有 $i$ 个权值 $>a[u]$,$u$ 的子树中边权和的最大值。
发现当 $1\le i<up[u]$ 时,当前状态中 $u$ 的父边可以 $>a[u]$,否则当前状态中 $u$ 的父边只能 $\le a[u]$。
那么也就相当于这么一个问题:有 $n$ 组物品,每组中都有 $2$ 个不能同时选的物品。
第 $i$ 组中有 $1$ 个花费为 $0$ ,价值为 $val[i][0]$ 的物品以及 $1$ 个花费为 $1$ ,价值为 $val[i][1]$ 的物品,
于是 $u$ 节点的所有状态就能用普通的背包转移了。
时间复杂度 $O(n^2)$。
## Subtask 7
考虑优化 $dp$ 状态。
$dp[u][0/1]$ 表示 $u$ 节点的父边权值 能 / 不能 $>a[u]$,$u$ 的子树中边权和的最大值。
同样求出 $val[i][0]$ 和 $val[i][1]$,此时发现这个问题可以贪心解决。
现在相当于有初始价值 $\sum val[i][0]$ 以及一些物品,每个物品花费都是 $1$,第 $i$ 个价值为 $val[i][1]-val[i][0]$。
对于 $0\sim up[u]$ 中的每一个数求出能获得的最大总价值。
那么直接按照 $val[i][1]-val[i][0]$ 从大到小排序,将后面 $<0$ 的舍弃掉,贪心求前缀和即可。
此时 $dp$ 值也很容易就能计算出来。
时间复杂度 $O(n\log n)$,可以通过本题。
当然也可以不排序,运用 $nth\_element$ 就能做到 $O(n)$,这里不再赘述。
# E. Yoshino
## Subtask 1
考虑暴力修改,暴力查询逆序对,复杂度 $\operatorname O(n^3)$。
## Subtask 2
将逆序对改用归并排序或权值树查询,复杂度 $\operatorname O(n^2\log n)$。
## Subtask 3
由于修改长度是 $1$,直接考虑使用树套树维护动态逆序对。在修改时查询 $[1,l-1]$ 区间大于原数的和 $[r+1,n]$ 区间小于原数的数的个数并减去,然后对新数做类似的查询并加上。在查询逆序对时,可直接输出。复杂度 $\operatorname O(n\log^2 n )$
## Subtask 4
显而易见,在值域缩小的同时,修改区间也随之缩小。
于是我们可以考虑对每个值建一个树状数组,如果对应位置有这个值,则树状数组该位置的值就是 $1$,否则是 $0$。
在修改时,对 $[1,l-1]$ 区间的每个值分别做一个查询并做一个后缀和,对 $[r+1,n]$ 区间的每个值也做一个查询并做一个前缀和,然后对每个值,我们就可以用 $\operatorname O(1)$ 的复杂度修改并维护了。
注意不要忘了清楚修改区间内部对逆序对的贡献,这部分可以暴力。
由于值域可以认为是 $\operatorname O(\log n)$,故此处的复杂度为 $\operatorname O(n\log^2 n)$。
## Subtask 5
由于第两次操作一就会重置一次,我们可以考虑直接用数学方法计算出修改的贡献。
对于奇数次操作,直接重置,逆序对清零。
对于偶数次操作,分为 $l<x$ 和 $l>x$ 两种。
如果 $l<x$,则我们修改完后的该区间的值为 $[x,x+r-l]$,易知 $[l,r]$ 与 $[x,x+r-l]$ 的交集为 $[x,l-1]$。
则对于值在 $[x,l-1] $ 区间的数,对逆序对的贡献显然是一个公差为 $-1$ 的等差数列,我们可以直接对此进行求和。
而对于值在 $[l,x-r+l]$ 区间的数,显然对逆序对没有贡献,直接忽略。
如果 $l>r$ 则类似讨论。
于是,我们就可以 $\operatorname O(1)$ 完成对逆序对个数的计数(注意此时我们并不需要直接修改这个数列),复杂度 $\operatorname O(n)$。
## Subtask 6
考虑颜色段均摊。
这是一种类似于珂朵莉树的 trick(事实上这就是珂朵莉树的推平操作),复杂度为均摊 $\operatorname O(n\times k)$,其中 $k$ 为单次修改的复杂度。
对于一个区间染色的操作,我们可以直接将一个区间维护为一个点,并且将他装入在 $set$ 或其他容器中。
在修改时,我们在 $set $ 中找到我们需要清除的所有区间(如果边界被包含则将边界所在的区间断开变成两个区间),并**暴力**将它们逐个清除,再插入新的区间。
为什么这样做的复杂度是正确的呢?我们可以来证明一下。
最初的时候,每个数单独构成一个区间,所以一共有 $n$ 个区间。
而每次操作的时候,我们增加的区间包括断开左右边界区间时增加的两个区间,以及插入的新区间。
这样一来,整个操作过程中区间的总个数就是 $n+3m$ 个。
而显然一个区间最多被插入一次,删除一次,且 $nm$ 同级,所以复杂度为均摊 $\operatorname O(n\times k)$。
本题中的操作一并不是颜色段均摊,但显然可以用类似的方法,均摊 $\operatorname O(n\times k) $ 完成修改。
但我们在修改的同时,还需要再维护一个动态逆序对,于是考虑令 $k=\log^2n$,使用树套树修改
考虑插入一个新段对逆序对的贡献(删除就将贡献减去)。
假设这个区间是 $[l,r]$,这个区间的值的范围是 $[x,y](r-l=y-x)$。
那么我们大致可以其他的数分为以下几类:
1. 位于 $[1,l-1]$ 区间且值小于 $x$ 的数。这类数没有贡献,直接无视。
2. 位于 $[r+1,n]$ 区间且值大于 $y$ 的数。这类数同样没有贡献,直接无视。
3. 位于 $[1,l-1]$ 区间且值大于 $y$ 的数。这类数对区间内的所有数都有贡献,只需统计个数并乘以 $r-l+1$。
4. 位于 $[r+1,n]$ 区间且值小于 $x$ 的数。这类数同样对区间内的所有数都有贡献,处理方法同上。
5. 位于 $[1,l-1]$ 区间且值位于 $[x,y]$ 之间的数。注意到,对于值为 $t(t\in[x,y])$ 的数,它对这个区间的贡献为 $t-x$,因为这个区间内前 $t-x$ 个数的值会小于 $t-x$。于是我们可以对**权值**维护区间内的个数以及区间和,也就是一个范围内值在某个区间的数有几个,以及这几个数加起来是多少。然后用和减去个数乘以 $x$ 就是我们所要的结果。
6. 位于 $[r+1,n]$ 区间且值位于 $[x,y]$ 之间的数。处理方式类似于第五类数。
这样一来,我们就在修改的同时完成了对逆序对的维护,而复杂度没有发生变化。
于是最终的复杂度就是 $\operatorname O(n\log^2 n)$。
## 总结
本题的难度并不高,没有涉及到很复杂的维护方法,也没有涉及到很高级的数据结构,主要还是对一些基本技巧的灵活应用。另外,有一个颜色段均摊的操作值得大家掌握。
为良心的出题人点赞!
# F
**性质 1**
将这个图分成 $nm$ 个 $2 \times 2$ 个正方形,那么每个正方形中恰好有一个 $1 \times 2$。
证明:称 $S$ 为所有被 $1 \times 2$ 覆盖的格子的集合,那么 $|S|=2mn$。每个这样的 $2 \times 2$ 中至多有两个格子属于 $S$。
然而所有 $4mn$ 个格子中,恰好有一半的格子属于 $S$。所以每个 $2 \times 2$ 中恰好 $2$ 个,构成一个 $1 \times 2$。
从左上角的格子开始依次考虑,可以证明这些就是所有的魔力之石。
-----
根据这个性质,称一个上述的分割中的 $2 \times 2$ 的方格为 **上,下,左,右** 之一,取决于 $1 \times 2$ 在它中的位置。
**性质 2**
一个 **上** 的方格的上方的方格也是 **上** 的,右边是 **上** 或者 **右**,左边是 **上** 或者 **左**。其他四种方格类似。
证明显然。
那么,结合以上两条性质,这个图大概是长这样的:

注意到,如果现在就要推式子等方法计算的话,这个生成函数肯定是二元的形式,难以计算,可以用矩阵做到 $\Theta(n^6 \log m)$ 的复杂度,不详细说明。
这一步需要极高的技巧,相当于因式分解了那个难以刻画的二元生成函数。
用两条路径刻画这个图,一条从左上到右下,一条从左下到右上:

那么分成的四块就恰好是 **上,下,左,右**。
现在这题变成:左上走到右下,每次向右或者向下,有些地方不能走,求方法数。
不能走是因为有 $k$ 个指定的位置,那么这些会限制这条路径。
当然,现在还没有明确说明哪些地方不能走,这里说清楚,下面的例子主要考虑左上到右下的路径。
限制就是,所有 **下** 的方格和所有 **左** 的方格和剩下两种方格被这条路径分成两半,也就是,如果把下和左看成 $1$,其余看成 $2$,那么这条路径将 $1$ 与 $2$ 分成两个部分。
现在让这个方格表左下为 $(0,0)$,右上为 $(m,n)$。如果一个 $1$ 类方格的左下角为 $(p,q)$,那么这条路径不能经过任何 $x\le p$ 并且 $y \le q$ 的点,对于 $2$ 类方格类似。下面的图表明了一种可能的能走与不能走的位置。

这里,红色的点表示不能走的点,绿色的线是一条合法的路径,黄色的线把能走到的地方分成了几个矩形。
矩形未必要有长与宽(可以为 $0$),可能用 $s\times t$ 的点阵($ s,t \ge 1$)来形容更加合适,下面 **点阵** 和 **矩形** 都代表这个意思。
这些矩形是有特殊要求的,不难发现不能走的地方构成了两个简单多边形,这两个多边形的边有水平的和竖直的,用竖直的边分割这个网格图得到了图中所示的矩形,后面的方法会说明为什么要这么分,可以通过上面的图更好的理解这些矩形是怎么刻画出来的。
当然,刻画这些矩形需要将所有放好的块排序并且利用单调栈维护,细节比较多,这里不细说。
考虑最基本的 `dp` 以及一个没有限制的图,令 $dp[i][j]$ 为到 $(i,j)$ 的合法路径数,那么 $dp[i][j]=dp[i][j-1]+dp[i-1][j]$。
这个式子可以化成 $dp[i][j]=\sum_{k=1}^jdp[i-1][k]$,也就是一个前缀和的形式。
注意到,如果按照上面的方式将合法区域划分为矩形,那么每个长为 $t$ 的点阵就相当于做 $t-1$ 次前缀和。
我们用到生成函数的知识,如果假设第 $i$ 列(横坐标为 $i$ 的所有点)从上到下的 $dp[i][j](0 \le j \le n)$ 构成生成函数 $F_i(x)=\sum dp[i][j]x^j$,其中 $0 \le i \le m$,我们有递推式:
$F_{i+1}(x)=\frac{F_i(x)}{1-x}$,如果第 $i$ 列与第 $i+1$ 列在同一个矩形内;
如果不在同一个矩形内,一定在相邻两个矩形内,设这两个矩形的上下高度分别为 $h_1,l_1,h_2,l_2$,如图:

那么,这个生成函数,就是先保留原来 $F_i(x)$ 在 $h_2$ 到 $l_1$ 次项的系数,然后对其做前缀和,为 $G_{i+1}(x)$,然后 $F_{i+1}(x)$ 的系数,不大于 $l_1$ 次项的与 $G_{i+1}(x)$ 相同,$l_1$ 到 $l_2$ 次项用 $G_{i+1}(x)$ 的 $l_1$ 次项系数填充。
这个比较难以用式子进行刻画,所以只能通过文字进行解释。
我们并不需要求出所有的 $F_i(x)$,因为需要的甚至只是 $F_m(x)$ 的一项系数,所以我们求出所有矩形两条宽所在列代表的多项式,相邻多项式之间的转移可以用多项式前缀和以及 $NTT$ 优化就可以在 $n \log n$ 的时间内完成,由于矩形一共 $\Theta(n)$ 个那么这是 $n^2 \log n$ 的,但是这不够优秀,瓶颈在求前缀和上。
如果不用做前缀和,剩下的操作甚至是 $\Theta(n)$ 的。我们考虑一个稍微一般一点的问题:
维护一个多项式,支持三种操作:
(1)做若干次前缀和;(2)查一项系数;(3)加上一个单项式。
(在同一个矩形内的转移规约为(1)操作,相邻矩形转移可以查询 $h_1$ 到 $h_2$ 次项所有系数并依次减掉对应的单项式,然后再做一次前缀和,然后查询 $l_1$ 次项的系数,最后在依次查询 $l_1+1$ 到 $l_2$ 次项的系数,把他们加上与 $l_1$ 次项的系数的差)
此时解法几乎呼之欲出了:
维护一个多项式 $Q(x)$ 与一个整数 $t\ge 0$,我们真实的多项式是 $\dfrac{Q(x)}{(1-x)^t}$,那么对于(1)操作直接修改 $t$,对于 $2$ 操作可以 $O(n)$ 求出卷积的一项,对于 $3$ 操作将这个单项式乘以 $(1-x)^t$ 后加到 $Q(x)$ 上即可,时间复杂度 $O(n^2)$。
关于作者Zhang, Xuheng
- 还没有填写个人简介
- Email: hy23682@126.com
- 注册于: 2020-04-07 05:11:14
