2019年Noip普及组复赛第四题解析

本文作者：Zhang, Xuheng  本文分类：编程学习笔记  浏览：1329
阅读时间：1504字, 约1.5-2.5分钟

题目如下：

分析:这道题目理解起来还是比较费劲的，题目大意就是说，如果一个人想生产一个L阶段的零件，那么与他相连的所有点必须都生产一个L-1阶段的零件给他，现在题目已知某一个点想要生产一个L阶段的零件，询问一号点是否需要提供原材料。
  首先，这道题目肯定是图论里面的题目，这没跑了，我们知道图论入门的时候学的就是dfs，bfs，地杰斯特拉，弗洛伊德，SPFA等等这几种算法，还有什么最小割，网络流之类的，要想知道该题目是否能用得上这些母版算法，我们还是得建立该题目的模型。

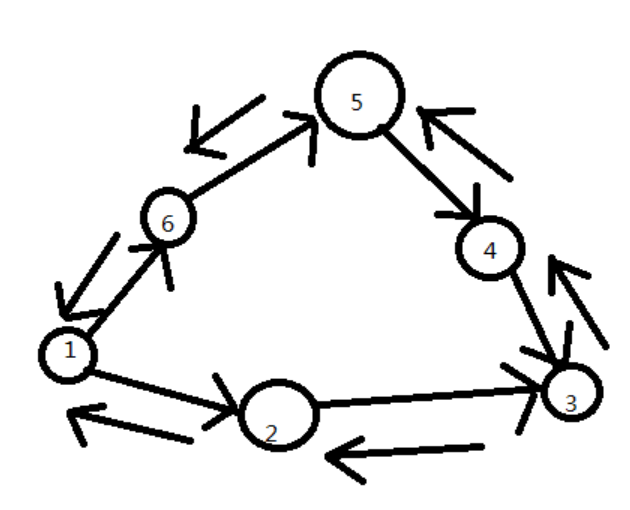
我们先来看一个图，现在比如3号点，想要生产一个L = 2 阶段的零件，那么2号点必须给他一个1阶段的，1号点必须给2号点原材料。
如果3号点想要生产一个4阶段的呢，那么2号点必须生产3阶段的，3号点必须生产2阶段的…这就又回到了上一个问题，我们总结可以得到，如果一个点跟一号点之间的最短偶数距离为L，那么如果这个点生产L+2，L+4，L+6…阶段的零件时，一号点必须提供给原材料。
同理，一个点跟一号点之间的最短奇数距离也有这个推论成立…
现在我们来总结一下，我们用两个数组来存储一个点到一号点之间的最短距离，一个存储最短奇数距离，一个存储最短偶数距离。
当询问的时候，我们就去查询这两个数组，如果是奇数，就去查询存放奇数最短距离的数组，如果是偶数就去查询存放最短偶数距离的数组。
至于怎么求最短路，方法就很多了，可以狄杰斯特拉，SPFA，bfs。我在这里就提供一种较为简单的bfs算法。

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
#define N 100010
using namespace std;

int ji[N],ou[N];
vector<int> v[N];
int n,m,q;


void bfs(){
    memset(ji,0x3f,sizeof(ji));//奇数最短路径
    memset(ou,0x3f,sizeof(ou));//偶数最短路径
    queue<pair<int,int> >q;
    for(int i=0;i<v[1].size();i++){
        ji[v[1][i]]=1;
        q.push(make_pair(v[1][i],1));
    }
    while(q.size()){
        int x=q.front().first,y=q.front().second;
        for(int i=0;i<v[x].size();i++){
            if(y%2==1){//奇数+1=偶数
                if(y+1<ou[v[x][i]]){
                    ou[v[x][i]]=y+1;
                    q.push(make_pair(v[x][i],y+1));
                }
            }else{//偶数+1=奇数
                if(y+1<ji[v[x][i]]){
                    ji[v[x][i]]=y+1;
                    q.push(make_pair(v[x][i],y+1));
                }
            }
        }
        q.pop();
    }
}



int main()
{
    cin>>n>>m>>q;
    for(int i = 1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        v[x].push_back(y); //采用邻接矩阵来存储图
        v[y].push_back(x);
    }
    bfs();  //跑一遍bfs得到答案
    while(q--){
        int a,l;
        cin>>a>>l;
        if(l%2 == 0){
            if(ou[a]>l) puts("No");
            else puts("Yes");
        }else{
            if(ji[a]>l) puts("No");
            else puts("Yes");
        }
    }
    return 0;
}

关于作者Zhang, Xuheng

• 还没有填写个人简介
• Email: hy23682@126.com
• 注册于: 2020-04-07 05:11:14