本文作者:Zhang, Xuheng
本文分类:编程学习笔记 浏览:1861
阅读时间:1010字, 约1-1.5分钟
题目如下:


10分:
#include<bits/stdc++.h>
using namespace std;
int t,n,m;
int main () {
cin>>t>>n>>m;
if (t == 1) {
cout<<m<<endl;
fclose(stdin);
fclose(stdout);
return 0;
}
cout<<endl;
fclose(stdin);
fclose(stdout);
return 0;
}
思路:
因为可以在第a天买入,第b天卖出,当然,b要大于等于a。这样收入就是price[b]-price[a] (我们假设用price数组来存储某个物品第i天的物品的价格),但是再去换个角度思考这个问题呢,我们假设一个人在第a天买入一个物品,第a+1天卖出这个物品,然后又买回来,在第a+2天又卖出去,当天再买回来…一直到第b天卖出去,不难发现,这样其实是跟在第a天买入,第b天卖出的效果是一样的,那么经过这样的转换有什么好处呢,一个好处就是我们把思考的范围缩小了,原来需要考虑好几天,现在我们只需要考虑怎么样才能保证今天买入在明天卖出的时候可以获利最大就好了,也就是说,我们只需要考虑隔一天获利最大就好了
代码如下:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define N 100010
typedef long long ll;
using namespace std;
ll t,n,m;
ll f[N]; //f数组来存储最大获利
ll price[101][N]; //用price数组来存储第i个物品第j天的时候的价格
int main(){
cin>>t>>n>>m;
for(int i = 1;i<=t;i++)
for(int j = 1;j<=n;j++)
cin>>price[i][j]; //读取数据
for(int i = 1;i<t;i++){ //做n-1次完全背包问题
memset(f,0,sizeof(f)); //每次做之前初始化f数组
for(int j = 1;j<=n;j++) //完全背包问题母版
for(int k = price[i][j];k<=m;k++){
f[k] = max(f[k],f[k-price[i][j]]+price[i+1][j]-price[i][j]);
}
m+=f[m]; //做完一次后加到现有的金币数上
}
cout<<m<<endl;
return 0;
}
关于作者Zhang, Xuheng
- 还没有填写个人简介
- Email: hy23682@126.com
- 注册于: 2020-04-07 05:11:14

主题操作记录:
2020-5-12 17:45审核通过
@EricNTH ( •̀ ω •́ )
题目描述
小伟突然获得一种超能力,他知道未来T天N种纪念品毎天的价格。某个纪念品的价格是指购买一个该
纪念品所需的金币数量,以及卖出一个该纪念品换回的金币数量。
每天,小伟可以进行以下两种交易无限次
1.任选一个纪念品,若手上有足够金币,以当日价格购买该纪念品;
2.卖出持有的任意一个纪念品,以当日价格换回金币
每天卖出纪念品换回的金币可以立即用于购买纪念品,当日购买的纪念品也可以当日卖出换回金币。当
然,一直持有纪念品也是可以的
T天之后,小伟的超能力消失。因此他一定会在第T天卖出所有纪念品换回金币。
小伟现在有M枚金币,他想要在超能力消失后拥有尽可能多的金币。
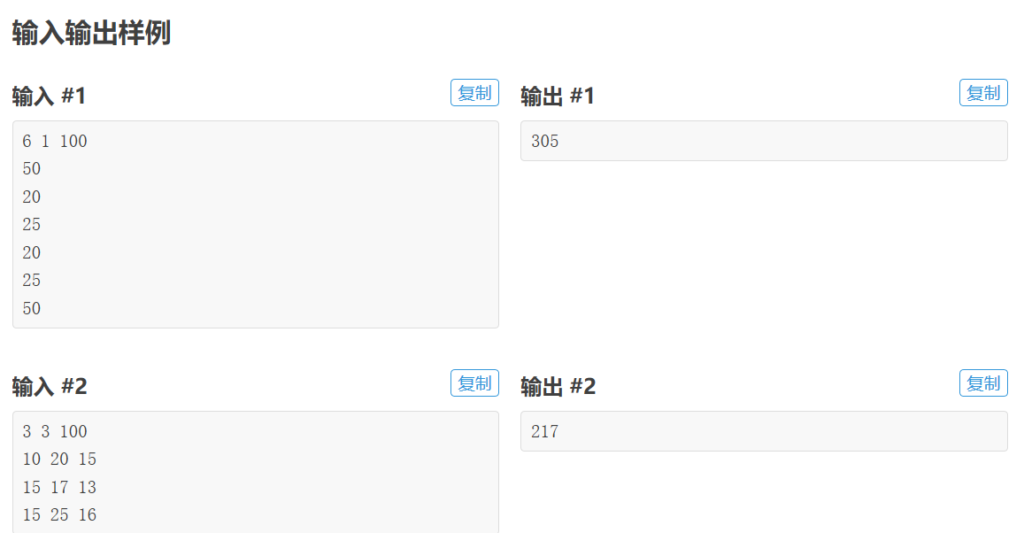
输入格式
第一行包含三个正整数T,N,M,相邻两数之间以一个空格分开,分别代表未来天数T,纪念品数量N
,小伟现在拥有的金币数量M.
接下来T行,每行包含N个正整数,相邻两数之间以一个空格分隔。第i行的N个正整数分别为P1
P2…P.N,其中P表示第讠天第j种纪念品的价格。
输出格式
输出仅一行,包含一个正整数,表示小伟在超能力消失后最多能拥有的金币数量。